Construction in Combinatorics via Neural Network

(This is a post translated from the original post I wrote last year.)

As a mathematician who also worked in the field of AI, I always wondered if it is possible to build AI models that helps mathematicians to solve their problems. Honestly, I don’t believe that current AI (like large transformer-based language models) can think. However, they are doing a lot of things, including drawing, writing, etc.

In this post, I’m going to introduce a paper titled Construction in Combinatorics via Neural Network written by Adam Zsolt Wagner, which used neural network to solve actual problem in mathematics. What he achieved is the following: use reinforcement learning to find counterexamples for some conjectures in graph theory. Before we deep dive into the paper, I’ll introduce some basics of reinforcement learning first.

Reinforcement Learning (RL) is an area of machine learning that is used to build AlphaGo, the world-best AI Go-player.¹ In the framework of RL, an agent (model) learns to do actions that maximizes certain rewards. For example, AlphaGo first compute the predicted probabilities of winnning for each spot that it can place, and put a stone at the position where the probability is maximized. Then the model’s parameters are updated based on the result of the game.

There are several RL algorithms, and they can be classified as follows.

• model-based vs model-free: Environment determines how the state changes when an agent do some action. If there’s a model for the environment, then we say that the algorithm is model-based, and model-free otherwise.

• value-based vs policy-based: Value is an expectation of return (cumulative rewards), and policy is a function that determines which action that agent should perform. Value-based method only learns the value function and choose a policy that maximizes the value function. Policy-based method only learns the policy function without value function. There are some algorithms like actor-critic that learns both.

In the paper, Wagner used cross-entropy method, which is model-free and policy-based. Here’s how the cross-entropy method works:

1. Based on the current policy network (model), generate $N$ episodes. Here we use Monte Carlo sampling.
2. Keep $k$ episodes with top-$k$ returns and throw out the remaining ones.
3. Use the $k$ episodes’ action as label and state as input to train policy network.
4. Repeat 1-3.

Cross-entropy method is simple and easy to implement. Also, it converges very well and less sensitive to the choice of hyperparameters compared to other value-based methods. However, it is hard to use when environment is complicated.

In the paper, he solved various problems like finding lower bound for the permant of 312-pattern avoiding 0-1 matrices, and covering problem for hypercube. However, we are going to introduce the results on the counterexamples for conjectures in graph theory.

The first conjecture is the following due to Aouchiche and Hansen [1], which is an inequality on graph’s spectrum, matching number, and a number of verticies

Conjecture (Aouchiche-Hansen) Let $G$ be a connected graph on $n\geq3$ verticies, with largest eigenvalue $\lambda_1$ and matching number $\mu$. Then

\[\lambda_1 + \mu \geq \sqrt{n-1} + 1.\]

Eigenvalues of a graph means eigenvalues of a Laplacian matrix of a graph, which is defined as

\[L = D - A\]

where $D$ is a degree matrix (diagonal matrix with degrees on each entry) and $A$ is an adjacency matrix. It is known that the eigenvalues of this matrix contains a lot of information on the graph itself: for example, the largest eigenvalue is 2 if and only if the graph’s connected components are nontrivial bipartite graphs. Matching number is a maximum number of edges of a matching of a given graph, which is a subgraph where each vertext has degree at most 1. The above conjecture proposes an inequality between these quantities.

How can we disprove it, using cross-entropy method? First, we encode a graph with $n$ vertices as a binary sequence of length $\binom{n}{2} = \frac{n(n-1)}{2}$ where each entry represents a connectivity of a single edge of a graph (1 means connected and 0 means disconnected). Then we generate a graph in an autoregressive manner as we do for machine translation. Based on the current sequence of length $k < \binom{n}{2}$, a neural network computes a probability that $(k+1)$-th edge is connected, and sample it based on the probability. By repeating this for $\binom{n}{2}$ times, we get a sequence that corresponds to a graph, and the reward of this graph is computed as follows.

\[r(G) = \sqrt{n-1} + 1 - \lambda_1(G) - \mu(G)\]

As you can see, the reward directly reflects the inequality, and the original conjecture is equivalent to $r(G) \leq 0$ for all graph $G$. So if we train our policy network again and again, it generates a graph with high reward, and eventually we may get a graph with $r(G) > 0$ - which is a counterexample of the conjecture.

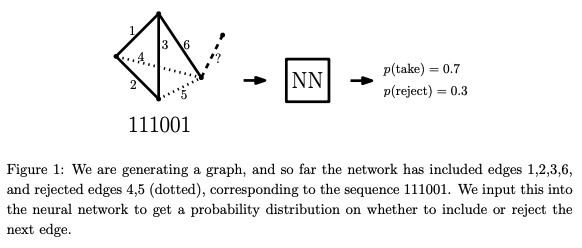
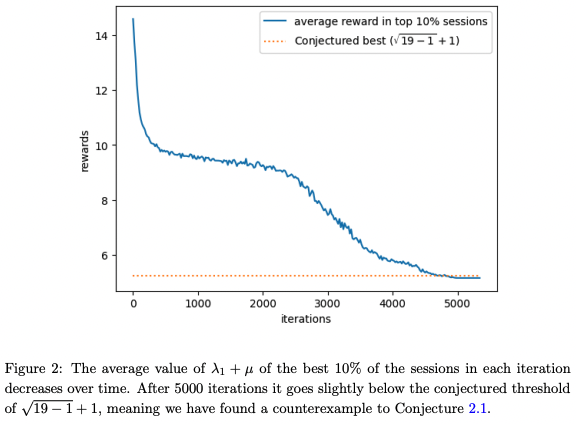
And he succeeded! He actually found a counterexample for $n = 19$. The below graph, whose $y$-axis represents $\lambda_1(G) + \mu(G) = -r(G) + \sqrt{n-1} + 1$, shows that the reward keeps increasing and at some point the model find a graph $G$ with $r(G) > 0$ - a counterexample.

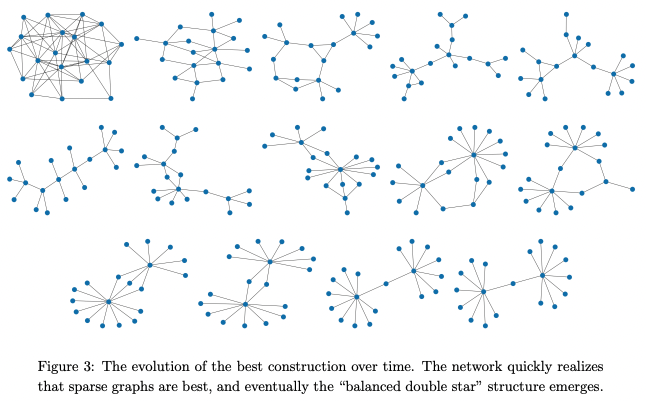
The following figure shows how the graph evolves during training. We can observe that it eventually converges to a graph called “balenced two stars”. In fact, it is known that the above conjecture is false before Wagner found his counterexample. However, the previous counterexample was a graph with 600 verticies, where Wagner’s counterexample has only 19.

Another conjecture (from the same people above) that is disproved in this paper is following inequality [2].

Conjecture (Aouchiche-Hansen) Let $G$ be a connected graph with $n\geq4$ verticies with diameter $D$, proximity $\pi$, and distance spectrum $\partial_1 \geq \cdots \geq \partial_n$. Then

\[\pi + \partial_{\lfloor \frac{2D}{3}\rfloor} \geq 0\]

Proximity of a graph is the minimum value of the average distance from a vertex to other vertices:

\[\pi(G) = \frac{1}{n-1} \min_{v\in V(G)} \sum_{w\in V(G)} d(v, w).\]

Distance spectrum stands for the eigenvalues of the distnace matrix of a graph, whose $(i, j)$-th entry is the distance between vertex $i$ and $j$. It is known that the following inequality holds [3]:

\[\pi(G) + \partial_{\lfloor \frac{D}{2} \rfloor} \geq 0\]

and Aouchiche-Hansen’s conjecture can be thought as a stronger version of this theorem. As you may expect, Wagner used the following function as a reward function and use cross-entropy method to find $G$ with $r(G) > 0$.

\[r(G) = -(\pi(G) + \partial_{\lfloor\frac{2D}{3} \rfloor})\]

Unfortunately, it was impossible to find a counterexample for $n \geq 30$ due to the limitation of computational resources. However, he found that the graph converges to the following shape:

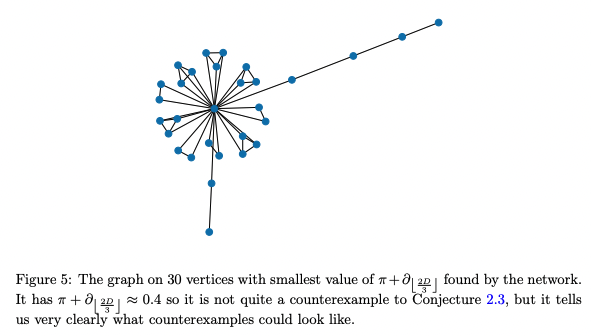
This strongly suggests us to try to find counterexamples among “double-tailed comet” shaped graphs. And he eventually found the following counterexample with 203 verticies (by hands).

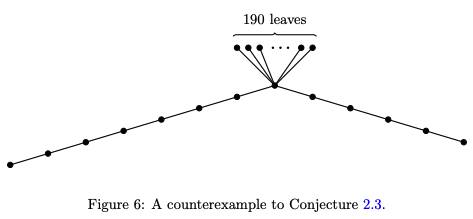
In the paper, there are some other results related to characteristic polynomial of a distance matrix and transmission regularity. I think the idea of this paper is really simple but meaningful since it showed that machine learning can be used to discover some mathematical results. Although there was a paper by Raayoni et al called Ramanujan machine [4] that generates some mathematical conjecture, I like Wagner’s paper more. It would be great if machine learning can be used to find counterexamples or give a hint to some well-known conjectures.

References:

[1] M. Aouchiche and P. Hansen, A survey of automated conjectures in spectral graph theory, Linear Algebra and its Applications (2010)

[2] M. Aouchiche and P. Hansen, Proximity, remoteness and distance eigenvalues of a graph. Discrete Applied Mathematics (2016)

[3] R. Merris, The distance spectrum of a tree, Journal of Graph Theory (1990)

[4] G. Raayoni et al. Generating conjectures on fundamental constants with the Ramanujan Machine, Nature (2021)

Tags: math  machine-learning