Relative Langlands Duality summer school & workshop at UMN

There was Relative Langlands Duality summer school & workshop at University of Minnesota, which introduces the recent work by Ben-Zvi, Sakellaridis, and Venkatesh (the huge paper called BZSV) and related works. I got interest in the topic after I study Gan-Gross-Prasad and Ichino-Ikeda type problems and related topics. In my understanding, relative Langlands duality can be summarized as

Study Langlands functoriality and relate it to periods and special L-values

as a number theorist, not as a mathematical physicist. But the “model” for relative duality comes from 4-dimensional boundary TQFT where boundary part explains period and $L$-functions. As far as I know, we don’t have nice arithmetic theory yet (we have arithmetic TQFT by Minhyong Kim, but they are not fully developed as much as geometric analogues), although we have a lot of known examples of the “P=L” conjecture for number field cases.

I wrote summary of each summer school and (subset of) workshop talks, based on my own notes and other’s notes. If there are anything wrong written below, it is due to my lack of understanding.

Summer school

There were four mini lecture series covering four different (but strongly connected) topics in relative Langlands duality.

1. Relative Langlands Duality - A-side by Yiannis Sakellaridis

Yiannis Sakellaridis introduced the A-side, i.e. Automorphic Side of relative Langlands duality. He started his (and the summer school’s) first lecture with drawing a turntable with A-side of an LP.

One of the main feature of relative Langlands program is that automorphic periods can be related to $L$-functions (or special $L$-values) on dual side. More precisely, let $G$ be a reductive group and $H$ be a spherical subgroup. Then $M = T^{\ast}(X) = T^{\ast}(H \backslash G)$ is a symplectic $G$-variety, and one can associate a dual symplectic variety $\check{M}$ with $\check{G}$-action on it. The following well-known examples fit into this phenomena:

Rankin-Selberg. $H = \mathrm{GL}_{n}$ is diagonally embedded into $G = \mathrm{GL}_{n} \times \mathrm{GL}_{n+1}$, and the dual space is $\check{M} = T^{\ast} (\mathrm{std}_{n} \otimes \mathrm{std}_{n+1})$. In this case, we have integral representation of $L$-function by Godment-Jacquet.

Gan-Gross-Prasad. $H = \mathrm{SO}_{n}$ is diagonally embedded into $G = \mathrm{SO}_{n} \times \mathrm{SO}_{n+1}$, and the corresponding dual is the tensor product of two standard representation, $\check{M} = \mathrm{std}_{n} \otimes \mathrm{std}_{n}$. In this case, we have Ichino-Ikeda conjecture of the form

\[\left|\int_{[\Delta \mathrm{SO}_{n}]} \varphi(h) \mathrm{d}h\right|^{2} = L\left(\pi, \mathrm{std} \otimes \mathrm{std}, \frac{1}{2}\right)\]

up to global constants and adjoint $L$-functions.

Whittaker. We have a unipotent group $N \subset G$ and a generic character $\psi: N \to \mathbb{C}^{\times}$, and $X = (N, \psi) \backslash G$. The dual is simply a point $\check{M} = \mathrm{pt}$ and the corresponding identity reduces to Lapid-Mao conjecture.

Group case. For $G = H \times H \supset H$ embeded diagonally, we have $X = H \backslash G \simeq H$. Then $\check{M} = T^{*}\check{H}$ and the corresponding $\check{G} = \check{H} \times \check{H}$ is not the naive action, but twisted by Chevalley involution. In thia case, one expect equation of the form

\[\int_{[H]} \varphi(h) \mathrm{d}h = \sum_{x} \sqrt{L(\pi, T_{x}\check{M})}\]

where the sum is over certain fixed points on $\check{M}$, and the square root of L-function can be make sense using adjoint $L$-functions.

Under the duality, one expect dual theorem by swapping $M = T^{*}(H \backslash G)$ with its dual. In GGP case, the dual theorem of Ichino-Ikeda conjecture becomes Rallis inner product formula for theta correspondence.

Sakellaridis also discussed about geometric case. Let $F = \mathbb{F}_{q}(\Sigma)$ be a function field of a curve over finite fields, and $G$ be a reductive group over $F$. For a spherical $G$-variety $X$, we have a space $\mathrm{Bun}_{G}^{X} \xrightarrow{p} \mathrm{Bun}_{G}$ that parametrizes $G$-bundles on $\Sigma$ and a $X$-section. Then the pushforward $p_{\ast} \underline{k}$ of a constant sheaf gives a sheaf on $\mathrm{Bun}_{G}$ is called the period sheaf $\mathcal{P}_{X}$, whose trace of Frobenius should recover theta series (of the distinguished unramified section). For the Iwasawa-Tate case ($G = \mathbb{G}_{m}$ and $X = \mathbb{A}^{1}$), $\mathrm{Bun}_{G}$ is simply the Picard group of $\Sigma$ and for the distinguished unramified section $\Phi = \mathbf{1}_{\hat{\mathcal{O}}}$, $\Theta_{\Phi}(g)$ counts the number of sections of the associated line bundle $\mathcal{L}_{[g]}$.

The remaining talks were about local periods and unramified Plancherel densities. Honestly, I could not understand this story well, so I recommend you to check other’s note on Sakellaridis’ third lecture.

2. Relative Langlands Duality - B-side by David Ben-Zvi

David Ben-Zvi introduced the other side of relative Langlands duality, which is B-side or Spectral side (or “B”alois side) - but actually he covered both sides later.

He stated relative Langlands as “studying the functoriality of Langlands correspondence”.For a reductive group $G$ over some field $F$, one can consider the automorphic theory or A-side of $G$, namely $\mathcal{A}_{G}$. Langlands functoriality is essentially about studying relations of $\mathcal{A}_{H}$ and $\mathcal{A}_{G}$ for different groups $H$ and $G$. More precisely, we want to upgrade the assignment $G \leadsto \mathcal{A}_{G}$ as a functor

\[H \xrightarrow{M} G \quad \leadsto \quad \mathcal{A}_{H} \xrightarrow{\mathcal{A}_{M}} \mathcal{A}_{G}.\]

Langlands program expect that automorphic theory for $G$ corresponds to a spectral theory for the dual group $\check{G}$ (over a coefficient field $k$), can be thought as algebraic geometry of Langlands parameters.. We denote this as $\mathcal{B}_{\check{G}}$ for $B$-side. One should also have a functoriality on spectral as well, and what we want is that the Langlands duality and functorialities are compatible.

What are $\mathcal{A}$ and $\mathcal{B}$? The model for this (in relative Langlands / BZSV) is 4-d TQFT. Ben-Zvi didn’t give any definitions of 4-d TQFT, but what he told us (which was enough for me) is the following: it assigns

• 3-manifold $\leadsto$ vector space,
• 2-manifold $\leadsto$ ($k$-linear) category,
• 1-manifold $\leadsto$ 2-category.

(He also mentioned that 4-manifold goes to a number in a base field, and I guess 0-manifold (point) maps to 3-category). Let’s denote the assignment (theory) as $\mathcal{Z}$. We also expect this to be a symmetric monoidal functor from the cobordism category: disjoint union corresponds to “products” (scalar product, tensor product, etc.) and manifolds with boundaries to morphisms between its values on those boundaries. $\mathcal{Z}(\Sigma \times \mathbb{S}^{1})$ is determined by $\mathcal{Z}(\Sigma)$ as the “dimension” or “cocenter”. More generally, if we have an automorphism $f: \Sigma \to \Sigma$ then it induces a morphism $\mathcal{Z}(f): \mathcal{Z}(\Sigma) \to \mathcal{Z}(\Sigma)$, and the trace of $\mathcal{Z}(f)$ recovers $\mathcal{Z}$ of mapping torus of $f$ (and $f = \mathrm{id}$ recovers $\Sigma \times \mathbb{S}^{1}$ case).

Hecke action can be given as follows. Given $\Sigma$, consider $\Sigma \times I = \Sigma \times [0, 1]$ and choose a small ball $\mathbb{S}^{2}$ centered at $(x, 1/2)$ (for $x \in \Sigma$). Then the disjoint union

\[\Sigma \bigsqcup \mathbb{S}^{2} \to \Sigma\]

yields

\[\mathcal{Z}(\Sigma) \otimes \mathcal{Z}(\mathbb{S}^{2}) \to \mathcal{Z}(\Sigma),\]

i.e. an action of $\mathcal{Z}(\mathbb{S}^{2})$ on $\mathcal{Z}(\Sigma)$. Moreover, we can “collapse” $\Sigma \sqcup \mathbb{S}^{2}$ over $I$ and get doubled $\Sigma$ with “ravioli” centered at $x \in \Sigma$:

\[\Sigma \to \Sigma_{x} := \Sigma \bigsqcup_{\Sigma \backslash \{x\}} \Sigma = \Sigma \bigsqcup_{D} (D \bigsqcup_{D^\times} D) \leftarrow \Sigma\]

giving a Hecke action at $x$. We can add more points and balls (raviolis) and compose these in three directions, giving $E_{3}$-algebra structure on $\mathcal{Z}(\mathbb{S}^{2})$. These are called observables $\mathrm{Obs}_{\mathcal{Z}}(\Sigma)$, acting on the states $\mathcal{Z}(\Sigma)$.

I haven’t mentioned what are $\mathcal{A}$ and $\mathcal{B}$ yet. (In geometric Langlands) $\mathcal{A}_{G}$ is referred to the topology of spaces of $G$-bundles, e.g. associate $\mathrm{Bun}_{G}(\Sigma)$ or its cohomology. $\mathcal{B}_{\check G}$ is on arithmetic geometry of moduli of local systems $\mathrm{Loc}_{\check G}(\Sigma)$, view as representations $\pi_{1}(\Sigma) \to \check G$ or locally constant maps $\Sigma \to B\check G$. Then (geometric) Langlands correspondence becomes

\[\mathcal{A}_G(\Sigma) \simeq \mathcal{B}_{\check G}(\Sigma)\]

in an appropriate sense. Moreover, Ben-Zvi mentioned the following diamond diagrams:

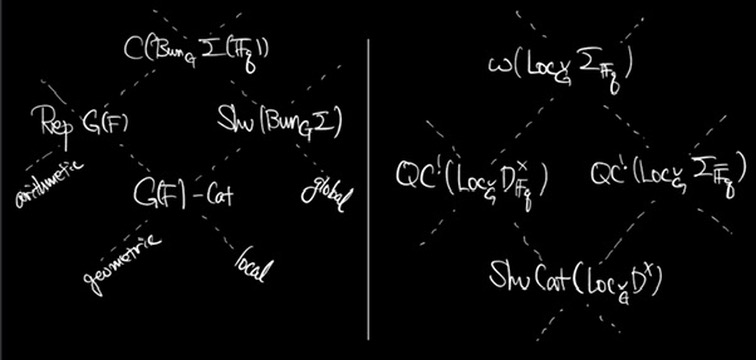
where

• $/$ direction corrsponds to local $\leftrightarrow$ global
• $\backslash$ direction corresponds arithmetic $\leftrightarrow$ geometric, via traces
• dimensions are 1, 2 and 3 from bottom to the top
• $\mathcal{A}_{G} \simeq \mathcal{B}_{\check G}$ duality holds for each vertex of diamond (left is $\mathcal{A}$, right is $\mathcal{B}$).

For relative Langlands, we need to relate $\mathcal{A}$ and $\mathcal{B}$-sides for different groups. Morphisms in field theory are interfaces, i.e. extension of two theories $\mathcal{Z}(\Sigma)$ and $\mathcal{Z}’(\Sigma)$ to a cylinder $\Sigma \times I$ (which is an analogue of bimodule). If $\mathcal{Z}’$ is a trivial theory, then the corresponding interface is the boundary theory for $\mathcal{Z}$, and it becomes 3-d TQFT if both $\mathcal{Z}$ and $\mathcal{Z}’$ are trivial. On $\mathcal{A}$-side, boundary theory correpsonds to periods, and the boundary theory on $\mathcal{B}$-side corresponds to L-functions ($\mathcal{L}$-sheaves). More precisely, L-functions become a (graded) traces of Frobenius of $\mathcal{L}$-sheaves, following Grothendieck’s function-sheaf correspondence.

Now, assume that two groups $G$ and $H$ acts on $X$ (like as a bimodule). Then we want to have a corresponding interface $\mathcal{A}_{X}$ with actions of $\mathcal{A}_{G}$ and $\mathcal{A}_{H}$ and similar for $\mathcal{B}_{\check X}$ with $\mathcal{B}_{\check G}$ and $\mathcal{B}_{\check H}$ actions. For example, Eisenstein series or Springer correspondence is encoded as $X = G / N$ with $G$ and $H = T$ actions on it. Unfortunately, we don’t know how to produce $\check X$ from $G, X, H$ in full generality yet.

Note that we have a similar arithmetic theory by Minhyong Kim, with analogy of

• 3-manifolds $\leftrightarrow$ number fields / global function fields / $\mathrm{Spec}(\mathcal{O}_{F})$
• 2-manifolds $\leftrightarrow$ local fields / curve over algebraically closed fields
• 1-manifolds $\leftrightarrow$ $\mathrm{Spec}(\overline{k}((t)))$, $\mathrm{Spec}(\mathbb{F}_{q})$.

Unfortunately, we don’t have a good theory of bordisms yet.

3. Relative Langlands Duality - Examples by Lei Zhang and Chen Wan

Lei Zhang and Chen Wan gave a ton of examples for relative Langlands duality. In relative Langlands, we have a notion of BZSV quadruple

\[\Delta = (G, H, \iota, \rho_H)\]

where $G$ is a (split) reductive group, $H$ is a (split) subgroup of $G$, $\rho_H$ is a symplectic representation of $H$, and $\iota: \mathrm{SL}_2 \to G$ is a homomorphism whose image commutes with $H$, so that it induces a map $\iota: H \times \mathrm{SL}_2 \to G$.

As we can associate Langlands dual group $\check{G}$ to a reductive group $G$, there exists a dual quadruple¹

\[\check{\Delta} = (\check{G}, \check{H}', \check{\iota}', \rho_{\check{H}'})\]

associated to $\Delta$. Some of the important points are:

• $\check{H}’$ is not equal to $\check{H}$ in general, and it is a group associated to whole $\Delta$, not just $H$.
• Unlike Langlands dual group (defined as swappring root datum), we don’t have a general systematic/algorithmic/combinatorial way to get $\check{\Delta}$ out of $\Delta$.

Now, the conjecture is that we have identities relating automorphic period of $\Delta$ (resp. $\check{\Delta}$) and certain $L$-values of $\check{\Delta}$ (resp. $\Delta$). More precisely, let $\pi$ be an automorphic representation of $G$ and $Y \subset V_{\rho_{H}}$ be the maixmal isotropic subspace. We can define the corresponding Weil representation $(\Omega_{\iota}, \mathscr{S}(Y(\mathbb{A})))$ of the metaplectic cover, and define the theta series $\Theta = \Theta_{\Omega_{\iota}}$ as usual:

\[\Theta(g) := \sum_{v \in Y(k)} \Omega_\iota(g) \phi(v), \quad g \in \mathrm{Mp}(V(\mathbb{A})), \quad \phi \in \mathscr{S}(Y(\mathbb{A}))\]

Then the automorphic period integral associated to $\Delta$ is given by

\[\mathcal{P}_{\Delta}(\phi) = \int_{[H]}^{\ast} \mathcal{F}_\iota(\varphi)(h) \Theta(\rho_{H}(h)) \mathrm{d}h\]

where $\mathcal{F}_{\iota}$ is a degenerate Whittaker period associated to $\iota$. Then we have the folloing “$\mathcal{P}_{\Delta} = L_{\check{\Delta}}$” conjecture:

1. $\mathcal{P}_{\Delta}(\varphi) \neq 0$ only if the Arthur parameter of $\pi$ factors through $\check{\iota} : \check{H}’(\mathbb{C}) \times \mathrm{SL}_{2}(\mathbb{C}) \to \check{G}(\mathbb{C})$.
2. Assume that $\pi$ is a lifting of a global tempered Arthur packet $\Pi$ of $H’(\mathbb{A})$. Then, up to a global constant, we have

\[\frac{|\mathcal{P}_\Delta(\varphi)|^{2}}{\| \varphi\|^{2}} = \frac{L(1/2, \Pi, \rho_{\check H'}) \prod_m L(m/2 + 1, \Pi, \check \rho_m)}{L(1, \Pi, \mathrm{Ad})^{2}}\]

Furthermore, we can obtain dual theorem/conjecture by swapping $\Delta$ and $\check \Delta$, i.e. $\mathcal{P}_{\check \Delta} = L_{\Delta}$.

There are a lot of known/conjectural examples, such as

• Lapid-Mao

\[\Delta = (G, 1, \iota_{\mathrm{reg}}, 0) \leftrightarrow \check \Delta = (\check G, \check G, 1, 0)\]

In this case, the dual theorem is trivial.

• Rankin-Selberg

\[\begin{align*} \Delta &= (\mathrm{GL}_n \times \mathrm{GL}_n, \mathrm{GL}_n^\Delta, 1, T^*\mathrm{std}) \\ \leftrightarrow \check \Delta &= (\mathrm{GL}_n \times \mathrm{GL}_n, \mathrm{GL}_n \times \mathrm{GL}_n, 1, T^*(\mathrm{std} \otimes \mathrm{std})) \end{align*}\]

We have

\[\mathcal{P}_{\Delta} = L_{\check \Delta} \Leftrightarrow \int_{[\mathrm{GL}_{n}^{\Delta}]} \varphi_{1}(h) \varphi_{2}(h) E(s, h, \phi') \mathrm{d}h = L(s, \pi_{1} \otimes \pi_{2}, \mathrm{std}_{n} \otimes \mathrm{std}_{n})\]

(for generic $\pi = \pi_1 \otimes \pi_2$). The dual theorem becomes Godment-Jacquet integral (theta correspondence):

\[\mathcal{P}_{\check \Delta}(\varphi) = \int_{[\mathrm{GL}_{n}]} \int_{[\mathrm{GL}_{n}]} \varphi_1(g) \varphi_2(g) \Theta(g, h) \mathrm{d}g \mathrm{d}h\]

(here $\Theta$ is the theta series for $\mathrm{Mp}_{2n^2}$) and it is nonvanishing if and only if $\pi_{2}$ is a global theta lifting of $\pi_{1}$ and $L(1/2, \pi_{1}) \neq 0$.

• Gan-Gross-Prasad

\[\begin{align*} \Delta &= (\mathrm{SO}_{2n+1} \times \mathrm{SO}_{2n}, \mathrm{SO}_{2n}^\Delta, 1, 0) \\ \leftrightarrow \check \Delta &= (\mathrm{Sp}_{2n} \times \mathrm{SO}_{2n}, \mathrm{Sp}_{2n} \times \mathrm{SO}_{2n}, 1, \mathrm{std} \otimes \mathrm{std}). \end{align*}\]

We have Ichino-Ikeda formula

\[|\mathcal{P}_{\Delta}(\varphi_1 \otimes \varphi_2)|^{2} = L\left(\frac{1}{2}, \pi_{1} \otimes \pi_{2}, \mathrm{std} \otimes \mathrm{std} \right)\]

The dual theorem becomes Rallis inner product formula for theta correspondence.

• Jacquet-Shalika

\[\begin{align*} \Delta &= (\mathrm{GL}_{2n}, \mathrm{GL}_{n}, [2^n], T^\ast \mathrm{std}) \\ \leftrightarrow \check \Delta &= (\mathrm{GL}_{2n}, \mathrm{GL}_{2n}, 1, \wedge^2 \oplus (\wedge^2)^\vee) \end{align*}\]

We have

\[\mathcal{P}_\Delta = L_\Delta \Leftrightarrow \int_{[\mathrm{GL}_{2n}]} \varphi(h) E(s, \wedge^2(h), f) \mathrm{d}h = L(s, \pi, \wedge^2)\]

where $E(s, g, f)$ is the Eisenstein series of $\mathrm{GL}(\wedge^2) = \mathrm{GL}_{n(2n-1)}$. Then the dual theorem becomes

\[\mathcal{P}\_{\check \Delta}(\varphi) = L(s, \tau) L(2, \tau, \mathrm{Ad})\]

when $\pi$ is the Speh representation $(\tau, 2)$ (one needs to regularize $\mathcal{P}_{\check \Delta}$).

The above part was covered by Lei Zhang (for two lectures), and the remaining half is covered by Chen Wan, which was elaborated in his workshop talk (see below).

4. Mathematical definition of Coulomb branches and Ring objects in the derived Satake category by Hiraku Nakajima

This talk is also inclined to mathematical physics that I could not understand most of the things. I strongly recommend you to follow other’s notes linked above.

The first talk is to understand the meaning of the following equation, which is the equation (3.13) from Gaiotto and Witten’s paper $S$-Duality of Boundary Conditions in $\mathcal{N}=4$ Super Yang-Mills Theory²

\[\mathcal{T}^\vee = (\mathcal{T} \times \mathcal{T}[G] \, \backslash\mkern-11mu /\!\!/\!\!/ G)^*\]

where

• $G$ is a reductive group
• $\mathcal{T}$ is a 3d $\mathcal{N} = 4$ SQFT with $G$-symmetry ($\mathcal{T}$ for “T”heory)
• $\mathcal{T}[G]$ is a “kernel” 3d $\mathcal{N} = 4$ SQFT (only depends on $G$)
• $\backslash\mkern-11mu /\mkern-6mu/ \mkern-6mu/$ is SUSY gauging
• $*$ is 3d mirror

The above equation tells us how to compute “dual theory”. The Coulomb branch $\mathcal{M}_{C}$ for 3d $\mathcal{N} = 4$ SUSY gauge theory for $(G, M)$ is defined using Borel-Moore homology of a fiber of a certain fiber bundle of affine grassmannian, when $M = T^{\ast} N$ is an anomaly free symplectic representation of $G$. Some examples with $G = \mathbb{G}_{m}$ is provided.

Also, there’s a notion of Higgs branch $\mathcal{M}_H$, and there’s a sort of duality between two branches: we expect ath $\mathcal{M}_{C}$ is smooth if and only if $\mathcal{M}_{H}$ is a point. 3d mirror $\mathcal{T}^\ast$ of a theory $\mathcal{T}$ is defined to be another SQFT with $\mathcal{M}_{C}(\mathcal{T}^{\ast}) = \mathcal{M}_{H}(\mathcal{T})$ and $\mathcal{M}_{H}(\mathcal{T}^{\ast}) = \mathcal{M}_{C}(\mathcal{T})$.

Workshop

There was a workshop followed by the summer school, introducing recent works related to relative Langlands duality and BZSV framework. Here I record summary of some of the talks that I was interested in.

Tony Feng - Rankin-Selberg unfolding for geometric periods

This talk is based on the work by Tony Feng and Jonathan Wang (paper). The duality conjecture in BZSV is rougly following: under the geometric Langlands duality (which is still conjectural, although it is claimed to be proven very recently)

\[D(\mathrm{Bun}_{G}) \simeq \mathrm{Coh}(\mathrm{Loc}_{\check{G}})\]

a period sheaf $\mathcal{P}_{X} \in D(\mathrm{Bun}_{G})$ of $X$ corresponds to an $L$-sheaf $\mathcal{L}_{\check{X}} \in \mathrm{Coh}(\mathrm{Loc}_{\check{G}})$ of the dual $\check{X}$. Especially, they verified the conjecture for

• Iwasawa-Tate case, $G = \mathrm{GL}_{1} \curvearrowright \mathbb{A}^{1}$ (self-dual),
• Hecke case, $G = \mathrm{GL}_{2} \curvearrowright X = \mathrm{GL}_{2} / \mathrm{GL}_{1} \leftrightarrow \check{G} = \mathrm{GL}_{2} \curvearrowright \mathbb{A}^{2}$,
• Rankin-Selberg case, $G = \mathrm{GL}_{2} \times \mathrm{GL}_{2} \curvearrowright X = \mathrm{Ind}_{\Delta \mathrm{GL}_{2}}^{\mathrm{GL}_{2} \times \mathrm{GL}_{2}} (\mathbb{A}^{2} \backslash {0})$ $\leftrightarrow$ $\check{G} = \mathrm{GL}_{2} \times \mathrm{GL}_{2} \curvearrowright \check{X} = (\mathbb{A}^{2} \otimes \mathbb{A}^{2})^{\mathrm{rk} \leq 1}$.

Note that $\check{X}$ in the Rankin-Selberg case is singular and non-affine, so it is not covered in the original BZSV conjecture. The main idea is to use Eisenstein case

\[G \times T \curvearrowright X = G / N \leftrightarrow \check{G} \times \check{T} \curvearrowright \check{X} = \check{G} / \check{N}\]

and the Whittaker case

\[G \curvearrowright X = G / (N, \psi) \leftrightarrow \check{G} \curvearrowright \check{X} = \mathrm{pt}\]

as building blocks, and mimic the standard unfolding process categorically. One needs to understand how $\mathcal{P}_{X_{1} \cup X_{2}}$ and $\mathcal{L}_{X_{1} \cup X_{2}}$ are related to $\mathcal{P}_{X_{1}}, \mathcal{P}_{X_{2}}$ and $\mathcal{L}_{X_{2}}, \mathcal{L}_{X_{2}}$, and the point is that one needs some “correction terms” or “thickenings” for these. The main tool is the derived Fourier transform developed by Feng-Yun-Zhang.

Spencer Leslie - Rationality and Stabilization for Symmetric Varieties

Friedberg and Jacquet proved the following BZSV-like result for the pair of groups

\[(G, H) = (\mathrm{GL}_{2n}, \mathrm{GL}_{n} \times \mathrm{GL}_{n})\]

where $H$ is embedded in $G$ block-diagonally. They proved that the following: let $\pi$ be a cuspidal automorphic representation of $G$. The automorphic period $\mathcal{P}_H(\phi) = \int_{[H]} \phi(h) \mathrm{d} h$ is nonvanishing for some $\phi \in \pi$ if and only if

1. $L(s, \pi, \wedge^2)$ has a pole at $s = 1$ (which corresponds to the factor-through-A-parameter condition in BZSV conjecture stated in Wan and Zhang’s talk)
2. $L(1/2, \pi) \neq 0$.

The main case of interest in Leslie’s ongoing work (joint with Jingwei Xiao and Wei Zhang) is the unitary version of Friedberg-Jacquet pair:

\[(G, H) = (\mathrm{U}_{2n}, \mathrm{U}_{n} \times \mathrm{U}_{n}).\]

and its arithmetic counterpart (the periods would be related to the base change $L$-function $L(1/2, \mathrm{BC}(\pi))$ in this case). The main obstacle for studying this case compared to Friedberg-Jacquet is that one needs a Galois action to distinguish this case with other twists. For example, for a quadratic extension $E /F$, the following two varieties

\[X_{1} = \mathrm{GL}_{2n} / (\mathrm{GL}_{n} \times \mathrm{GL}_{n}), \quad X_{2} = \mathrm{GL}_{2n} / \mathrm{Res}_{E/F} \mathrm{GL}_{n}\]

are isomorphic over $E$, but not over $F$. The action of $\mathrm{Gal}(E/F)$ on the first three components of their dual datum ($\check{G}, \check{G}_{\Delta}, \check{\iota}$) cannot distinguish those two, hence one needs Galois action on $\check{\rho}$.

To do this, they defined inner and outer forms for $G$-varieties (as in a way that we may expect), and propose the following theorem to distinguish outer forms.

Theorem (Leslie). Let $G$ be a quasi-splic group over $F$, fix Borel $B \subset G$, and $X = G / H$ a spherical variety ($H$ is a spherical subgroup of $G$). Let $\mathrm{Aut}^{\mathrm{dist}}(X)$ be the distinguished automorphism group defined by Losev. $\Gamma = \mathrm{Gal}_F$.

1. There exists a canonical 1-cocycle $c_X: \Gamma \to \mathrm{Aut}^{\mathrm{dist}}(X)(\overline{F})$ such that for two $G$-varieties $X_1$ and $X_2$ that are $G$-forms each other, they are $G$-inner if and only if $[c_{X_1}] = [c_{X_2}]$.
2. Let $X = G / G^\eta$ be a symmetric variety, associated to an involution $\eta: G \to G$. Then $\mathrm{Aut}^{\mathrm{dist}}(X)$ determines a symplectic representation $\check{G}_{X} \curvearrowright S_{X}$ and the data of $c_{X}$ uniquely determines further $\Gamma$-action, hence ${}^{L} \check{G}_{X} \curvearrowright S_{X}$.

For example, in case of $X_1$ and $X_2$ above, we have $c_{X_1} = 1$ but $c_{X_2}: \Gamma \to {\pm 1}$ is a quadratic character.

Furthermore, for the symmetric case, we can tell something about endoscopy. More precisely, for a semisimple and suitably Galois-stable $s \in \check X$, one has an endoscopic datum $e = (G_{\mu(s)}, \mu(s), \xi)$ and $X_e = G_{\mu(s)} / H_e$ for some stabilizer $H_e$ and a canonical $F$-rational map between categorical quotients

\[X_e // H_e \xrightarrow{\varphi_e} X // H,\]

which is what we need for the stabilization of the relavent RTF. Leslie mentioned that they proved weak transfer and the fundamental lemma.

Chen Wan - Strongly tempered BZSV quadruples

This talk is based on the work by Zhengyu Mao, Chen Wan, and Lei Zhang (paper). They focus on strongly tempered BZSV quadruples, which are $\Delta = (G, H, \iota, \rho_H)$ where their duals have a form

\[\check{\Delta} = (\check{G}, \check{G}, \check{\iota}, \check{\rho})\]

(up to center - to be precise, it should be $\check{H}$ with $\check{G} = \check{H} Z_{\check{G}}$.) Also, we call $\Delta$ reductive if $\iota = 1$. In this case, the $L$-factors correspond to $\mathrm{SL}_{2}$-part in the dual side vanishes and the period-L-function conjecture becomes

\[\frac{|\mathcal{P}_{\Delta}(\phi)|^{2}}{\langle \phi, \phi \rangle} = \frac{L(1/2, \pi, \check{\rho})}{L(1, \pi, \mathrm{Ad})}\]

(of coures, up to a global and ramified factors). The most famous example of strongly tempered case is the GGP case, where we have

\[\begin{align*} \Delta &= (\mathrm{SO}_{2n+1} \times \mathrm{SO}_{2n}, \mathrm{SO}_{2n}, 0, 1) \\ \leftrightarrow \check{\Delta} &= (\mathrm{Sp}_{2n} \times \mathrm{SO}_{2n}, \mathrm{Sp}_{2n}, \times \mathrm{SO}_{2n}, \mathrm{std} \otimes \mathrm{std}, 1) \end{align*}\]

Now, we know that $(\check{G}, \check{G}, \check{\rho}, 1)$ is a BZSV quadruple if

1. $\check{\rho}$ is anomaly-free,
2. $\check{\rho}$ is multiplicity-free,
3. the generic stabilizer of $\check{\rho}$ of $\check{G}$ is connected.

Luckily, we have a classification of multiplicity-free symplectic representations by Knop. Hence this gives “tables” of the dual quadruples $\Delta$, and our question is to find the corresponding $\Delta$ (as I mentioned before, there’s no algorithmic or combinatorial way to find dual quadruple of a given BZSV quadruple yet.) Mao, Wan, and Zhang give many tables of conjectural correspondances, and provide three tyles of evidences:

1. local character formula for the dual pairs
2. prove the P=L conjecture assuming (refined) GGP and Rallis inner product formula
3. behaves well under “Whittaker induction”³

For 3, their Whittaker induction is defined as follows. The map $\iota : \mathrm{SL}_{2} \to G$ defines a parabolic subgroup $P = MN$ where $M$ is a centralizer of the image of $\mathrm{diag}(t, t^{-1})$ and

\[N = \{ g \in G : \lim_{t \to 0} \iota(\mathrm{diag}(t, t^{-1})) g \iota(\mathrm{diag}(t, t^{-1}))^{-1} = 1\}.\]

As before, $\iota: H \times \mathrm{SL}_{2} \to G$ defines an adjoint action of $H \times \mathrm{SL}_{2}$ on $\mathfrak{g}$ and decompose it as

\[\mathfrak{g} = \bigoplus_{k \geq 0} \rho_{k} \otimes \mathrm{Sym}^{k}.\]

Then we define $\Delta = (G, H, \iota, \rho_H)$ to be the Whittaker induction of $\Delta_{0} = (M, H, 1, \rho’)$ where

\[\rho' = \rho \oplus \left(\bigoplus_{k \,\mathrm{odd}} \rho_k \right)\]

Then the third evidence reads as follows. Assume that the dual quadruple of $\Delta_0$ is $\check{\Delta}_0 = (\check M, \check M, 1, \rho_{\check M})$, i.e. strongly tempered. If $\rho_{\check M}$ is an irreducible representation of $\check M$ with highest weight $\varpi_{\check M}$, then we define $\rho_{\check M}^{\check G}$ to be the irreducible representation of $\check G$ with highest weight $\varpi_{\check G} = w \varpi_{\check M}$ for some $w \in W_G$. If $\rho_{\check M}$ is not irreducible, do this for all the irreducible factors. Then they conjectured that $\check \Delta = (\check G, \check G, 1, \rho_{\check M}^{\check G})$. They checked that, all the quadruples $\Delta$ in Table 3-6 are Whittaker inductions of some other quadruples $\Delta_{0}$, and if we assume the conjectural duality for $\Delta_{0}$ and $\check{\Delta}_{0}$, then the above conjecture is also true.

Charlotte Chan - Generic character sheaves on parahoric subgroups

The talk covered several papers by Chan and coauthors (possibly all the papers in Chan’s webpage with “Deligne-Lusztig” in abstracts).

Deligne-Lusztig theory gives a way to build irreducible representations of reductive groups over finite fields via cohomology of Deligne-Lusztig varieties. Once we have a representation $\pi$ of such groups $G(\mathbb{F}_{p})$, the easiest(?) way to produce a representation of $p$-adic groups $G(\mathbb{Q}_{p})$ is 1) to take pullback along the natural map $G(\mathbb{Z}_{p}) \twoheadrightarrow G(\mathbb{F}_{p})$ and 2) take a compact induction to $G(\mathbb{Q}_{p})$. However, we can only obtain depth 0 representations of $G(\mathbb{Q}_{p})$ in this way.

To get representations of positive depths, Adler and Yu boost up the step 1) of the above construction, which is “algebraic” in nature. Instead, one may consider to use representations of “thickened” groups $G(\mathbb{Z} / p^{r}\mathbb{Z})$ using “geometry”. These are called jet schemes: more precisely, for a connective reductive group $G$ over $\mathbb{F}_{p}$, we define the $r$-th jet scheme $G_{r}$ as a group scheme $A \mapsto G(A[t] / t^{r+1})$. Then there’s an analogous jet-version of Deligene-Lusztig variety whose cohomology gives a representation of $G_{r}(\mathbb{F}_{p})$, and following the remaining step gives irreducible cuspidal representations of $G(\mathbb{Q}_{p})$ of positive depth.

Now, the main slogan is: Yu’s algebraic construction is, on geometric side, given by parabolic induction. For a charater $\theta : T \to \mathbb{F}_p^\times$, we have a parabolic induction $\mathrm{pInd}_T^G(\theta)$ and a class function associated to it:

\[g \mapsto \sum_{\substack{hB \in G / B \\ hgh^{-1} \in B}} \theta(\mathrm{pr}(hgh^{-1}))\]

where $\mathrm{pr}: B \to T$ is the projection. One can categorify this as follows: let

\[X = \{(g, hB) \in G \times G/B: hgh^{-1} \in B\}\]

with two projections $\pi : X \to G$ (the natural projection) and $f: X \to T, (g, hB) \mapsto \mathrm{pr}(hgh^{-1})$. Then the sheafification of the above class function is simply $\mathrm{pInd}_T^G(\mathcal{L}_\theta) := \pi_{!} f^{\ast} \mathcal{L}_\theta$, where $\mathcal{L}_\theta$ is a local system on $T$ associated to $\theta$. Lusztig proved that this is a simple perverse sheaf, and taking trace of Frobeinus recovers the class function associated to $R_T^G(\theta)$. Lusztig conjectured that the same is true for jetified version, and this is what Chan and other collegues proved (e.g. see Bezrukanikov and Chan). One interesting point is that, when we match up the geometric construction with Yu’s algebraic construction, it requires some correction that arises in local Langlands. Chan also mentioned that, one can take limit of (cohomology of) jetified Deligne-Lusztig varieties, and the result is related to $p$-adic Deligne-Lusztig variety.

Zhiwei Yun - Character sheaves in the setting of theta correspondence

Theta correspondence (over finite fields) is roughly given by the following way. Let $(V_{1}, w_{1})$ and $(V_{2}, q_{2})$ be symplectic and orthogonal spaces. Taking a tensor product gives a bigger symplectic space $(V, w) = (V_{1} \otimes V_{2}, \omega_{1} \otimes B_{q_{2}})$, with a represenetation of $G_{1} \times G_{2} = \mathrm{Sp}(V_{1}, w_{1}) \times \mathrm{O}(V_{2}, q_{2})$. Now, choose a nontrivial character $\psi: \mathbb{F}_{q} \to \mathbb{C}^{\times}$ and a Lagrangian $L \subset V$, and consider a Weil representation $\omega = \omega(\psi, L)$ of $\mathrm{Sp}(V, w)$ attached to $(\psi, L)$ (following Shrödinger model). Now, Waldspurger proved that the restriction $\omega|_{G_{1} \times G_{2}}$ decomposes as multiplicity one factors, and this gives so-called theta correspondence between irreducible repsentations of $G_{1}$ and $G_{2}$ by

\[\omega|_{G_{1} \times G_{2}} = \bigoplus \pi \boxtimes \Theta(\pi), \quad \pi \in \mathrm{Irr}(G_{1}),\,\, \Theta(\pi) \in \mathrm{Irr}(G_{2}).\]

(Note that Weil representations for other fields may require metaplectic covers, but we don’t need this over finite fields.)

Now, in my understanding, the goal of this talk (based on a joint work with Shamgar Gurevich) is about geometrization of theta corresspondence - the irreducible projectors above correspond to perverse sheaves on $(V_{1} \otimes V_{2}) / (G_{1} \times G_{2})$. Especially, one can construct $\Theta$-sheaves analogous to $\Theta$-correspondence. There’s a notion of parabolic induction for $\Theta$-sheaves, and the building blocks for $\Theta$-sheaves are Cayley sheaves that live on $\mathbb{A}^{2} / \mathbb{G}_{m}$ (the action is hyperbolic). Finally, one can construct character sheaves from $\Theta$-sheaves by taking pullback along $G_{1} \times G_{2} \times V \twoheadrightarrow V$, take a tensor product with Gurevich-Hadani’s kernel sheaf, and than pushforward along $G_{1} \times G_{2} \times V \to G_{1} \times G_{2}$.

Concluding remarks

While staying at Minnesota, I learned that relative Langlands is an extremly active area and a lot of people are working on it. The workshop hugely motivated myself, and I decided to study meterials including

• perverse sheaves (it seems that perverse sheaves are “linear algebra” of geometric Langlands, and I can’t say anything without knowing about it)
• dual of spherical variety (Knop-Schalke)
• the original GGP paper and SV (not BZSV) paper
• Mao-Wan-Zhang’s paper (see if there’s any example that is more interesting than other examples)

which are more than enough for remaining years.

Also, there’s a Korean restaurant called Korea Restaurant, and it was an authentic and great (I ate 도가니탕). Hongkong Noodle was a good choice, too.

Tags: math