How to not to be a coward

I saw the following proof today (from Twitter, and also from my friend):

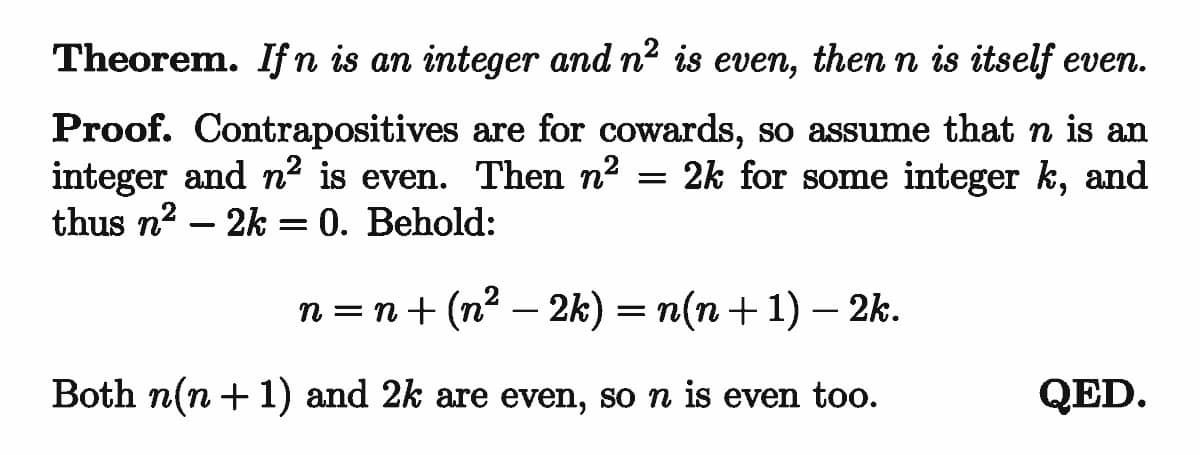
Now, here’s a question: consider a multiple of $3$ instead. We still have $n^2 \equiv 0 \pmod{3} \Rightarrow n \equiv 0 \pmod{3}$. Can we prove this, but not being a coward? How about mod $5$?

The answer is yes. Try to do it yourself before you click the triangle below.

Proof

$$ \begin{align*} n &= n^{2} \cdot n - (n-1)n(n+1) \qquad (m = 3) \\ n &= n^{2} \cdot (n^{3} - 5n) + 5n - (n-2)(n-1)n(n+1)(n+2) \qquad (m = 5) \end{align*} $$ and use the fact that product of consecutive $k$ integers are always a multiple of $k$ (in fact, $k!$).

In this post, we will show that similar proof works for all prime and higher powers:

Theorem. For prime $p$, $\mathbb{Z} / p\mathbb{Z}$ has no nilpotent elements. In other words, for $k \ge 2$, $n^k \equiv 0 \pmod{p}$ implies $n \equiv 0 \pmod{p}$.

First of all, we can reduce to the case when $k = 2$. For given $k$, take $a$ with $2^{a} \ge k$. Then we have $n^{2^{a}} = (n^{2^{a} - k}) n^{k} \equiv 0 \pmod{p}$. From $n^{2^a} = (n^{2^{a-1}})^{2}$, we have $n^{2^{a-1}} \equiv 0 \pmod{p}$, and repeating this gives $n \equiv 0 \pmod{p}$.

For $k = 2$, our goal is to express $n$ as a $\mathbb{Z}$-linear combination of integer-valued polynomials, which are (i) divisible by $n^2$, or (ii) every value is divisible by $p$. As above,

\[\begin{align*} f(n) &= n(n+1)(n+2) \cdots (n+(p-1)) \\ &= n^{p} + a_{p-1} n^{p-1} + \cdots + a_{2} n^{2} + a_{1} n \end{align*}\]

is a multiple of $p$ for any $n$. We have $a_{1} = (p-1)!$, and by Wilson’s theorem, $a_{1} + 1 = (p-1)! + 1$ is a multiple of $p$. Hence

\[n = n^{2}(n^{p-2} + a_{p-1}n^{p-3} + \cdots + a_{2}) + (a_{1} + 1)n - f(n)\]

is divisible by $p$. $\square$

The theorem is still true if one replace $p$ with square-free integers. In fact, the decomposition for $p = 3$ gives a proof for mod $6$, too. Unfortunately, I don’t know if there’s a general construction of a combination for square-free modulus case.

Tags: math