ChatGPT5.2-Pro proved something for me

The goal of this post is to share an experience where ChatGPT5.2-Pro (Extended Thinking mode) genuinely helped me prove a small lemma.

Question

I wanted to prove the following statement:

Lemma. Let $g(t) = t^8 e^{-t}$ and $f(t) = \sum_{n \ge 1} g(nt)$. Then $f(t)$ is monotone decreasing on $(0, \infty)$.

Here’s a plot of the graph that shows its monotonicity on $2.5 < t < 20$.

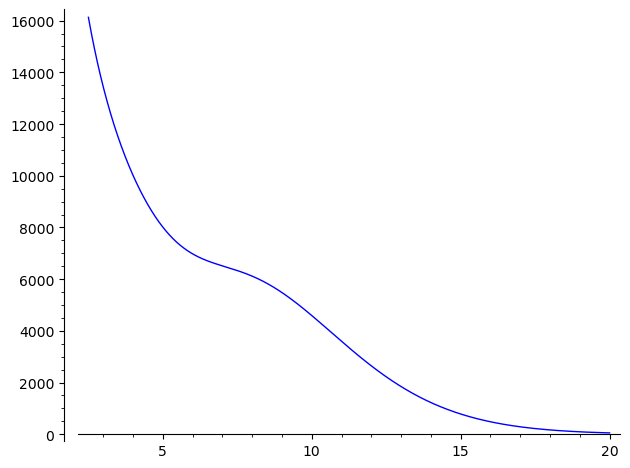
You can see that the function looks quite weird (it is not completely monotone). I wanted to show this in a clean way (without numerical analysis), but such a wiggly graph suggests that there might not be such a proof. The reason I needed the Lemma was to prove the following claim:

Proposition. Let $X_{10, 1}$ be Kaneko-Koike’s extremal quasimodular form of weight 10 and depth 1. Then the function

\[t \mapsto t^8 X_{10, 1}(it)\]

is monotone decreasing on $(0, \infty)$.

Lemma $\Rightarrow$ Proposition follows by considering a Lambert series expansion of $X_{10, 1} = E_8’ / 480$ (here $E_8$ is the Eisenstein series of weight 8). Using this, one can prove

Theorem. For even $w \ge 6$, let $X_{w, 1}$ be Kaneko-Koike’s extremal quasimodular form of weight $w$ and depth 1. Then the function

\[t^{w - \lceil w/6\rceil} X_{w, 1}(it)\]

is monotone decreasing on $(0, \infty)$.

I expect that the exponent $8$ or $w - \lceil w/6\rceil$ is not optimal. In fact, I conjecture that

Conjecture. For even $w \ge 6$ and $w \ne 8, 10$, let $X_{w, 1}$ be Kaneko-Koike’s extremal quasimodular form of weight $w$ and depth 1. Then the function

\[t^{w - 1} X_{w, 1}(it)\]

is monotone decreasing on $(0, \infty)$.

One can show that $w - 1$ is the largest possible exponent for those $w$’s. All of this will appear in a future paper (and also my thesis). If you wonder why such statements matter, stay tuned (you can already find an answer somewhere).

What I tried (without AI)

The goal in proving the Theorem above is to give a weak result toward the Conjecture with a reasonable exponent not far from $w - 1$. Note that monotonicity of $t \mapsto X_{w, 1}(it)$ (without a polynomial factor) follows from the depth-1 case of the Kaneko-Koike conjecture, which is proved in this paper (Corollary 4.4). The most annoying part is that the conjecture fails for $w = 8, 10$, which can be checked rigorously by examining the behavior of $t^7 X_{8, 1}(it)$ and $t^9 X_{10, 1}(it)$ for small enough $t > 0$ (if they were monotone decreasing, then the recurrence relation—Theorem 4.3 and Remark 4.5 of that paper—would imply the Conjecture; Proposition $\Rightarrow$ Theorem uses the same idea but with the correct claims).

I can prove monotonicity of $t^5 X_{6, 1}(it)$ and $t^6 X_{8, 1}(it)$ using the same idea, where the Lambert series expansion reduces them to the monotonicity of a rational function in $t$ and $e^t$. This can be shown in a boring but less analytic way by considering derivatives and proving inequalities of the form $P(t, e^t) > 0$ for a polynomial $P(x, y)$, manually decomposing them into sums of obviously positive functions.

Unfortunately, the same idea did not work for the Lemma: the corresponding rational function $f(t)$ is monotone, but I could not find a clean decomposition. I also considered higher derivatives, but they only made the expressions more complicated.

What I tried (with AI)

So I simply asked ChatGPT5.2-Pro to prove the Lemma; more precisely the query was the following:

Prove that the function

$$

t \mapsto t^8 * e^(-t) * ((e^(-7t) + 1) + 247 (e^(-6t) + e^(-t)) + 4293 (e^(-5t) + e^(-2t)) + 15619 (e^(-4t) + e^(-3t))) / (1 - e^(-t))^9

$$

is monotone decreasing for t > 0.

The expression can be handled with geometric series (though differentiating the formula eight times is not fun). ChatGPT noticed that the coefficients are Eulerian numbers and identified the function with $f(t)$ above. It then gave a proof of a stronger claim with $t^8$ replaced by $t^9$, which is false (see the plot below). So whatever it wrote could not be correct.

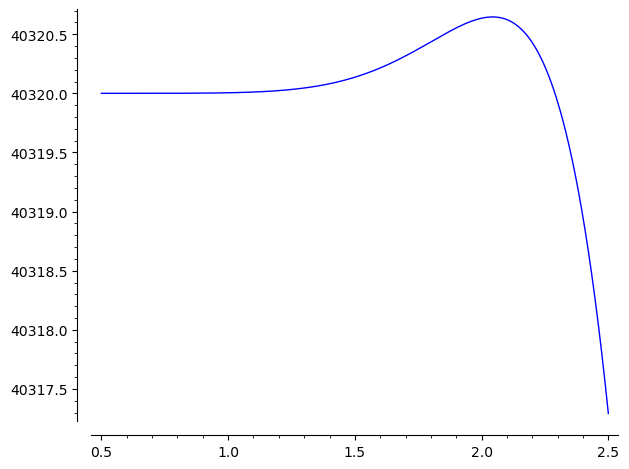
I pointed this out, and ChatGPT tried again; the proof looked better but still had a sign error. Then I asked Gemini 3 Pro the exact same question, and it produced the same (first) incorrect proof as ChatGPT. Since proving the Lemma itself was not critical, I put this aside and moved on to more interesting things.

After two months, I was annoyed that “prove this monotonicity” had been sitting on my TODO list, so I decided to try again. Instead of giving the expression, I (well, Sage) differentiated it and asked to prove that the (negation of the) denominator is positive:

Give a rigorous proof that the function

t*e^(8*t) + 502*t*e^(7*t) + 14608*t*e^(6*t) + 88234*t*e^(5*t) + 156190*t*e^(4*t) + 88234*t*e^(3*t) + 14608*t*e^(2*t) + 502*t*e^t + t - 8*e^(8*t) - 1968*e^(7*t) - 32368*e^(6*t) - 90608*e^(5*t) + 90608*e^(3*t) + 32368*e^(2*t) + 1968*e^t + 8

is positive for t > 0.

It “thought” for 75 minutes (a new record!) and told me that I could simply look at the Taylor expansion at $t = 0$. In particular, the $n$-th coefficient is positive for $n \ge 65$ (since all the linear terms are positive), and $1 \le n \le 64$ can be checked directly. The calculation was correct, and I double-checked it with Sage, so I am done and can finish the paper soon—and put ChatGPT in the acknowledgments.

What I learned

I have my own rule of thumb: I only use AI for boring tasks (including literature searches, to see if a result is already known or follows from a standard but unfamiliar technique) and never for interesting problems I want to tackle myself. In this case, the Lemma fell into the “boring” category, so I did not hesitate to ask. It still made me feel silly when I realized I had not thought of the Taylor expansion approach (probably because I never took a calculus course). However, the proof is not easily hand-checkable — even though it is algebraic in some sense — and it does not give new insight (for example, it cannot be used to prove the Conjecture for general $w$ for modular-form reasons). Nevertheless, it saved me time and lets us focus on more interesting things.